Research Areas
- Experimental physics in Wave Propagation in Complex Media
- Light-Matter Interaction
- Multiple Scattering, Anderson Localization
- Nonlinear and Active Random Media
- Random Lasers
- Nonlinear Scattering
- Instabilities
- Speckle Statistics
- Optical Singularities
- Optics
- Acoustics
- Microwaves
[tabs]
[tab title=”Active Control Of Random Laser”]
 |
Wave propagation in disordered media is a field of research with both fundamental important topics as well as a large range of applications related to imaging through opaque media, an important issue in medical imaging. |
[/tab]
[tab title=”Metamaterials With Flexural Waves”]
Metamaterials with Flexural Waves  |
By replacing atoms with man-made elementary structures, new artificial materials may provide novel functionalities. These so-called metamaterials may bend waves in an unusual manner (“negative refraction”), hide objects (“cloaking”), focus light below the diffraction limit |
[/tab]
[/tabs]
News.
Member of professor Patrick Sebbah research team, Ph.D. Chenni Xu has been awarded by the Israel Academy of Sciences and Humanities and the Council for Higher Education the Excellence Fellowship for International Postdoctoral Researchers. Our congratulations.
Latest Publications.
Ray engineering from chaos to order in two-dimensional optical cavities
Chenni Xu, Li-Gang Wang and Patrick Sebbah
Laser & Photonics Reviews, 2200724 (2023)
Chaos, namely exponential sensitivity to initial conditions, is generally considered a nuisance, inasmuch as it prevents long-term predictions in physical systems. Various approaches have been brought up to control or depress chaos.
Here we propose a new method to switch off deterministic chaos and tailor light ray trajectories in arbitrary 2D optical cavities, from the perspective of transformation optics. This method is accomplished by introducing spatially varying refractive index therein, where its landscape is obtained via a conformal transformation from integrable flat billiards. The irregular trajectories in the otherwise chaotic cavities therefore inherit the integrable features of the latter, with deterministic chaos eliminated in the cavities.
Moreover, trajectory rectification can be pushed a step further by relating chaotic billiards with non-Euclidean geometries. Two examples are illustrated by projecting billiards built on a sphere as well as the deformed spacetime outside a Schwarzschild black hole, which respectively lead to all periodic orbits and spiraling trajectories away from the boundaries of the transformed 2D billiards/cavities. An implementation of our method is proposed, which enables real-time control of chaos and could further contribute to a wealth of potential applications in the domain of optical microcavities.
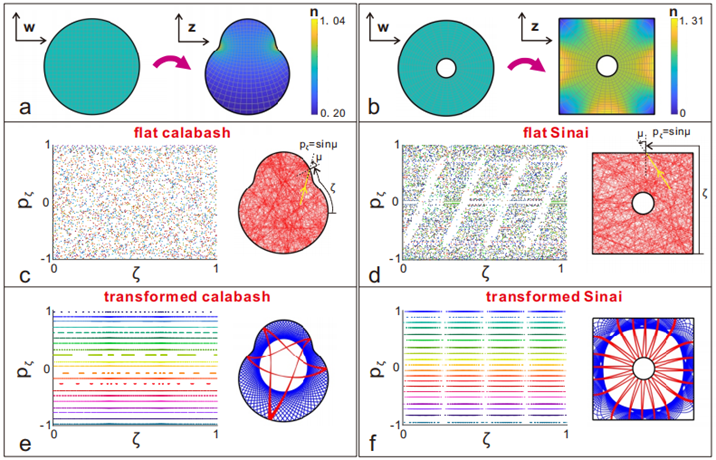
Switching off chaos in 2D chaotic billiards
(a,b) Transformation from a flat circular (a, left)/annulus (b, left) billiard to a calabash-shaped (a, right)/Sinai (b, right) billiard with nonuniform refractive index. (c-f) Poincaré SOSs of flat calabash-shaped (c), flat Sinai (d), transformed calabash-shaped (e) and transformed Sinai billiard (f).
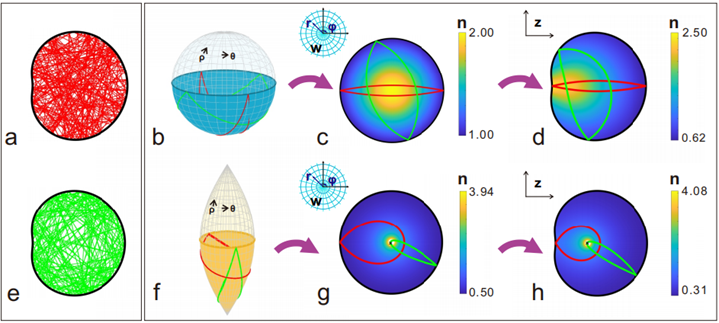
Realization of periodic trajectories transformed from non-Euclidean billiards
(a,e) Typical trajectories of light rays in planar Robnik billiards are chaotic. (b) A spherical billiard and (f) a spindle billiard. These billiards can be projected to inhomogeneous circular billiards (c,g), and further conformally transformed to Robnik billiards (d,h).
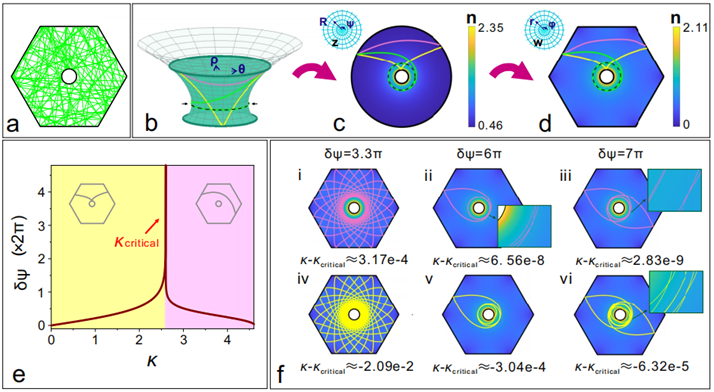
Spiraling trajectories transformed from Schwarzschild black hole
A typical trajectory of light rays in the planar hexagonal billiard. (b) 2D visualization of reduced Schwarzschild metric, which can be projected to an inhomogeneous circular billiard (c), and further conformally transformed to (d). (e) The angular distance δψ each trajectory completes between two successive collisions on the upper/outer boundary versus κ of different trajectories. (f) Trajectories with different δψ in real space.
Light chaotic dynamics in the transformation from curved to flat surfaces
Chenni Xu, Itzhack Dana, Li-Gang Wang and Patrick Sebbah
PNAS 119, e2112052119 (2022)
Light propagation on a two-dimensional curved surface embedded in a three-dimensional space has attracted increasing attention as an analog model of fourdimensional curved spacetime in the laboratory. Despite recent developments in modern cosmology on the dynamics and evolution of the universe, investigation of nonlinear dynamics of light on non-Euclidean geometry is still scarce, with fundamental questions, such as the effect of curvature on deterministic chaos, challenging to address. Here, we study classical and wave chaotic dynamics on a family of surfaces of revolution by considering its equivalent conformally transformed flat billiard, with nonuniform distribution of the refractive index. We prove rigorously that these two systems share the same dynamics. By exploring the Poincaré surface of section, the Lyapunov exponent, and the statistics of eigenmodes and eigenfrequency spectrum in the transformed inhomogeneous table billiard, we find that the degree of chaos is fully controlled by a single, curvature-related geometric parameter of the curved surface. A simple interpretation of our findings in transformed billiards, the “fictitious force”, allows us to extend our prediction to other classes of curved surfaces. This powerful analogy between two a priori unrelated systems not only brings forward an approach to control the degree of chaos, but also provides potentialities for further studies and applications in various fields, such as billiards design, optical fibers, or laser microcavities.
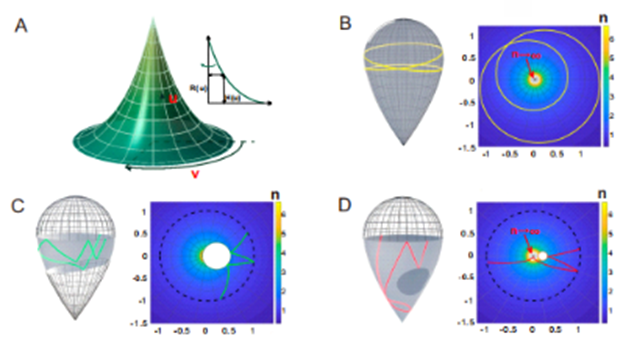
Sketch of Tannery surface and its projection
(A) Sketch of a typical SOR with the orthogonal curvilinear coordinates on it. (B) Tannery surface with c=2 (Left) and its projected billiard (Right). (C, D) Truncated Tannery surfaces with different means of truncation. The equators are denoted by black dashed lines in the projected billiards.
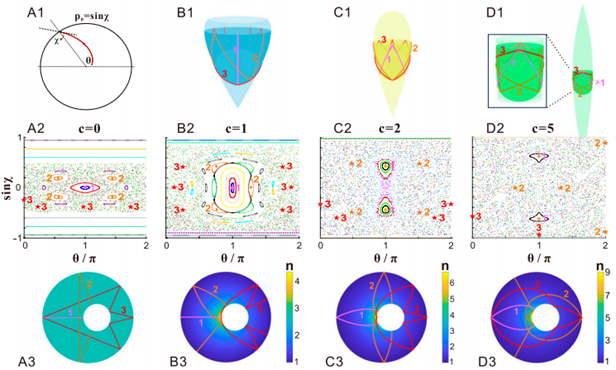
Poincaré surfaces of section of Tannery surfaces with different geometric parameter c
(A1) Sketch of Birkhoff coordinates. (B1, C1, D1) Sketches of Tannery surfaces with c=1, 2, 5, respectively. (A2, B2, C2, D2) Poincaré surfaces of sections of Tannery surfaces with c=0, 1, 2, 5, respectively. The diamonds and pentagrams, respectively, indicate typical stable and unstable POs. These POs in real space are exhibited in A3, B3, C3, D3, respectively, corresponding to the points with the same label and color.
Spiraling trajectories transformed from Schwarzschild black hole
A typical trajectory of light rays in the planar hexagonal billiard. (b) 2D visualization of reduced Schwarzschild metric, which can be projected to an inhomogeneous circular billiard (c), and further conformally transformed to (d). (e) The angular distance δψ each trajectory completes between two successive collisions on the upper/outer boundary versus κ of different trajectories. (f) Trajectories with different δψ in real space.
Pulse dynamics of flexural waves in transformed plates
Kun Tang, Chenni Xu, Sébastien Guenneau and Patrick Sebbah
Advanced Functional Materials 31, 2009266 (2021)
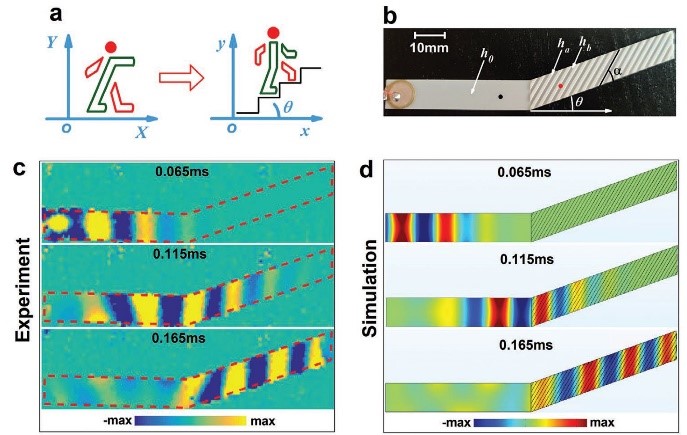 Dynamics of pulse propagation in the waveshifter. (a) Sketch of the coordinate mapping, (b) Top view of the waveshifter. (c) Experimental demonstration and (d) numerical simulation. | 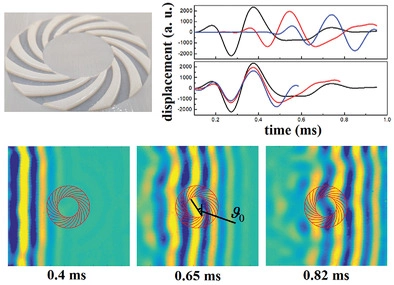 Dynamics of pulse propagation in the rotator. (a) 3d-printer elastic rotator. (b) Absence of temporal dispersion. (c) 30o rotation experienced by the elastic wave within the rotator and wave front recovery outside the rotator. |
Coordinate-transformation-inspired optical devices have been mostly examined in the continuous-wave regime: the performance of an invisibility cloak, which has been demonstrated for monochromatic excitation, is likely to deteriorate for short pulses.
Here, pulse dynamics of flexural waves propagating in transformed plates is investigated. A practical realization of a waveshifter and a rotator for flexural waves based on the coordinate transformation method is proposed. Time-resolved measurements reveal how the waveshifter deviates a short pulse from its initial trajectory, with no reflection at the bend and no spatial and temporal distortion of the pulse.
Extending the strategy to cylindrical coordinates, a wave rotator is designed. It is demonstrated experimentally how a pulsed plane wave is twisted inside the rotator, while its wavefront is recovered behind the rotator and the pulse shape is preserved, with no extra time delay. The realization of the dynamical mirage effect is proposed, where an obstacle appears oriented in a deceptive direction.
Observations of symmetry induced topological mode steering in a reconfigurable elastic plate
K. Tang, M. Makwana, R. V. Craster, P. Sebbah
Phys. Rev. B 102, 214103 (2020)
We investigate vibrational interface modes on elastic plates, to observe distinctive valley-Hall edge states. We have designed a reconfigurable system using clamped holes to create strong scatterers and interfaces that strongly confine vibration. At the physical scales we use here we can scan the field at points throughout the entire plate and extract the mode shapes. Our experimental observations of topological valley transport for sharp and gentle bends and the topological mode coupling around the gentle bend for flexural waves (see Figure), highlight key differences between sharp and gentle bends and the importance of the relative orientations of inclusion sets on either side of the interface. The direct visualization of the mode patterns through spatial scanning of the wavefield, linked with the underlying principles at the junction cells, sheds light on the transport of energy around bends in partitioned media. This important new observation, also confirmed here by theory and simulation, exposes the coupling required for geometrically distinct modes to move from one interface to another.
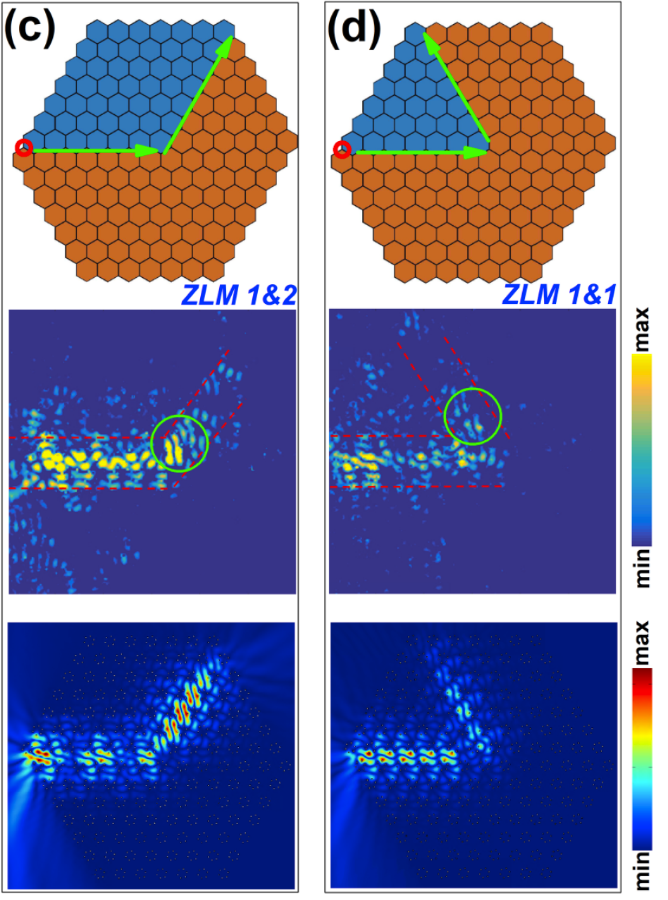 Gentle bend and sharp bend geometry in an elastic plate. Experiment demonstration and numerical simulation of edge states steering |
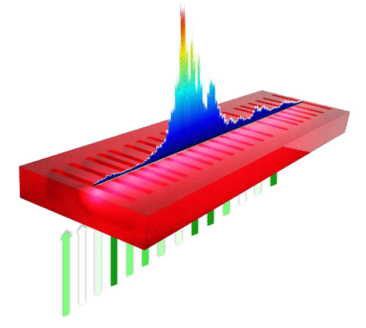
Localized modes revealed in Random Lasers
Bhupesh Kumar, Ran Homri, Priyanka, Santosh Maurya, Mélanie Lebental, and Patrick Sebbah
Reference: Optica 8(8), 1033-1039 (2021)
A collection of obstacles randomly positioned can be sufficient to trap light, without the need for an optical cavity. Add gain/amplification and you obtain -at no cost- a mirrorless laser, often dubbed “random laser”.
Here, we have used this concept to demonstrate disorder-induced localization, a rather difficult wave phenomenon to observe, but also one of the most striking and puzzling manifestations of wave interference, predicted by the Nobel Prize winner P.W. Anderson for electrons and later generalized to light waves. Because this faint phenomenon is amplified in our “plastic microlaser”, we directly observe laser light built up in confined scattering region, each confined mode corresponding to a different emission color/wavelength.
To observe these localized lasing modes individually, we propose a new method to disentangle interacting modes and suppress mutual competition for gain. To do so, a non-uniform gain distribution is created that optimally select one mode and extinguish the other.
Once mode competition is suppressed and a laser mode is optimized, we are able to boost laser power-efficiency, and unleash the “optimally-outcoupled lasing modes”, i.e. the laser modes with the strongest emission for the smallest energy cost.
 |
